The other day, I saw the word game Wordle going around on my Twitter feed. The game prompts you to guess a 5-letter word in a Mastermind-like style - every letter in your guess is reported as being correct, as present (i.e. that letter occurs somewhere in the answer, but is misplaced), or as absent.

As is my way, I immediately started thinking about how I could use this as a prompt for a small tech project. I considered making a bot to play the game (using Greasemonkey and KeyboardEvents), but the interface aspect is less interesting than the underlying strategy. What’s the best way to play the game?

Strategy

There is a limited universe of “answer candidates”¹. Every time you guess, the set of answer-candidates is divided into (3^5=)243 different partitions², based on the 3 possible states each of the 5 letters in your guess might be in:

• All answers for which all letters in your guess would be entirely incorrect
• All answers for which the first letter of your guess is present-but-incorrectly-placed, and all other answers in your guess are incorrect
• All answers for which the first letter of your guess is correct, and all other letters are incorrect
• All answers for which the first letter of your guess is correct, the second is present-but-incorrectly placed, and all others are incorrect
• …and so on…

This might be easier to understand with the following diagram:

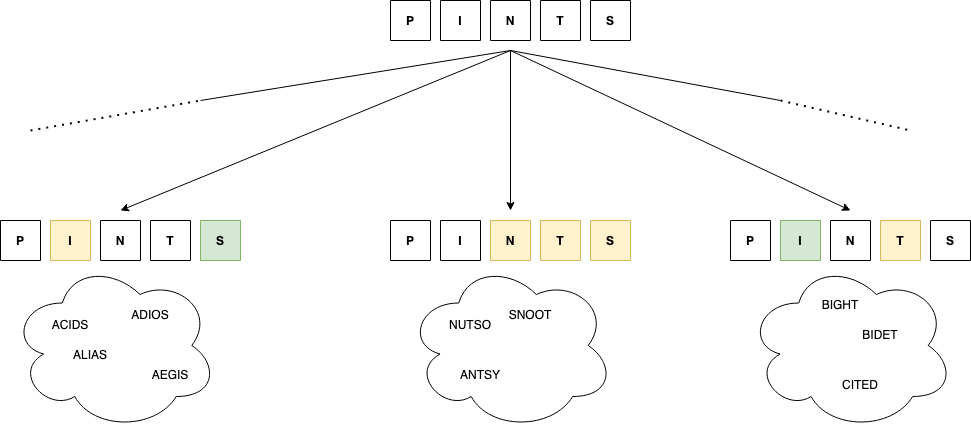
(Examples generated with this script)

The game’s response to your guess indicates which partition the answer lies in. Assuming that you haven’t guessed the word, you can then repeat the process with a different guess - your guess will tell you which “sub-partition” within that partition the word lies in, and so on. With each guess, you are gaining information that is used to reduce the set of possibilities. The strategy, then, is to determine which words you should pick to maximize the information gained at each step³.

Information is maximized when the size of the indicated partition is minimized⁴ - the smaller the indicated partition, the less uncertainty exists about which candidate is the actual answer. However, since we don’t know in advance which partition will be indicated (because we don’t know the answer), we instead have to minimize the expected partition size for all possible answers, rather than minimizing the size of the indicated partition (being able to do the latter would be equivalent to knowing the answer in advance!). For a given partioning strategy, we can calculate the expected partition size with the following (where “part(x)” is “the partition that contains (candidate answer) x”, $ \mathbb{P} $ is the set of partitions, and $ \mathbb{C} $ is the full set of candidate answers)⁵:

$$ \begin{aligned} E(size\ of\ partition) &= \sum_{c \in \mathbb{C}} \mathcal{P}(c\ is\ correct) * | part(c) |\newline &= \sum_{p \in \mathbb{P}} \sum_{c \in p} \mathcal{P}(c\ is\ correct) * |part(c) |\newline &= \sum_{p \in \mathbb{P}} \sum_{c \in p} \mathcal{P}(c\ is\ correct) * |p|\newline &= \sum_{p \in \mathbb{P}} |p| \sum_{c \in p} \mathcal{P}(c\ is\ correct)\newline &= \sum_{p \in \mathbb{P}} |p| \sum_{c \in p} \frac {1} {|\mathbb{C}|}\newline &= \sum_{p \in \mathbb{P}} |p| * \frac {|p|} {|\mathbb{C}|}\newline &= \frac {1} {|\mathbb{C}|} \sum_{p \in \mathbb{P}} |p|^2 \end{aligned} $$

Therefore, we can maximize the information gained at each guess by picking a guess that minimizes the sum-of-squares of the sizes of all resultant partitions. This strategy should then be repeatable to narrow down to the actual answer, by using the identified partition as the next “universe” of guessable words.

Conclusion

With this code, I figured out the best and worst words to start with (lower numbers are better):

Computing: [#############################################] 10657/10657
Best guesses:
(0.023954023202981775, 'roate')
(0.02416039632596131, 'soare')
(0.02440110277138952, 'salet')
(0.025732265392850645, 'orate')
(0.026118142082110753, 'earst')

Worst guesses:
(0.4011596826033615, 'immix')
(0.3858660533939142, 'jugum')
(0.38409863366438246, 'qajaq')
(0.375986639859308, 'gyppy')
(0.3756119588186725, 'fuffy')

Intuitively, these seem reasonable. The letters R, O, A, T, E, and S are all pretty common, so it makes sense to me that starting with words that use these letters would be optimal (particularly since, then, you’re more likely to get a “correct” letter, which is more informative than a “present” one). The worst guesses not only use rarer letters (J, X, Q, Y), but also use duplicated letters which give less information.

That said, I would love to do some testing on this strategy, by setting up the iterated strategy, having it “play” the game, and recording how may attempts are required to win. It would be particularly cool to see if there are cases where the second guess of this iterated strategy is known to be wrong (from the results of the first guess) because that increases the amount of information gained. If we know that the word ends in “E”, there’s more information gained by guessing a word that doesn’t end in E - but humans (probably?) intuitively try to “keep the known letters”. Maybe a follow-up post!

In particular, I’ve been informed (while writing this post) that a friend-of-a-friend had already figured out the optimal start-words, and they’re similar-to-but-different-from mine - so, there’s at least one interesting alternative perspective out there! (EDIT: 2021-12-29) I implemented an alternative approach - finding pairs of 5-letter words that together comprise the 10 most common letters in the corpus - which I’ve been told is pretty similar to Bruno’s (I intentionally waited until after I’d got two implementations before I spoiled myself by reading those tweets!), though we somehow got different answers. I’m looking forward to learning what I did wrong!

• wordle